The Softmax Function
The softmax function is a multi-dimensional extension to the sigmoid function that projects an incoming vector to a unit simplex. Therefore it is quite frequenly used in logistic regression (classification) tasks to represent the multinomial distribution over the data classes.
Mathematically, it is represented as \(\sigma(x_i)=\frac{e^{x_i}}{\sum_j e^{x_j}}\) and in the \(2\)-D case looks something like the figure below.
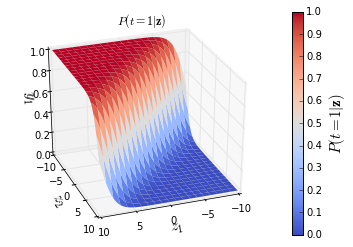Figure 1: Notice the flat surfaces (as \(y_1 \to 0\) and \(y_1 \to 1\) ).
Saturation in Softmax
As shown in figure 1, (very loosely speaking) softmax assigns very limited subset of values (from the input range) a probability mass that is significantly away from \(1\) or \(0\), i.e. the slope of the neck of the curve is too steep. While this is not particularly a bad thing, it can greatly hinder learning in first order stochastic gradient update type methods as the gradients around the flatter surfaces become too small to be usefull. This occurs very frequently in non-linear models like deep neural networks and as a result various alternatives to the softmax functions have been proposed like relu, elu, etc that can resolve the saturation problem. While these solutions might solve the saturation issue but they surely cannot be used to replace the softmax function in cases where an explicit probability distribution is required by the model. In one of our recent papers, we describe one such model. Inspired by our findings, in this post I will try to provide some intuition about the saturation issue and how to adapt the softmax function in order to resolve the slowdown of learning with respect to saturation.
De-constructing Softmax: General class of simplex projection methods.
For the context of this post, it would help to think of the softmax function as a method for unit-simplex projection. When it comes to simplex projection view of the softmax, what has always intrigued me is the arbitrary choice of using the number \(e\). So let’s de-construct the softmax function and see if there are other way of putting things back together such that they still sum to one without the saturation issue of the softmax function.
more tomorrow…